Dasar Metode Lagrange

Lagrange

Selasa, 28 April 2015

 

 

a.         Tentukan Koordinat Umum

 

Contoh Sistem

 

(V=0)

Sistem 1

 

 

 

 

 

 

 

 

 

 

Dalam sistem 1 diatas koordinat umum yang tak gayut dengan  yang  lain hanya terdapat 1 koordinat umum yaitu (θ , x, s) sedangkan koordinat variabel menentukan posisi dari sistem.

 

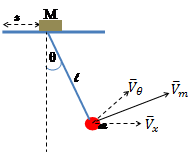
Sistem 2

 

 

 

 Pada sistem 2 ayunan dengan tumpuan pada benda (M) yang bebas bergeser

Koordinat umum         q₁= x à menentukan massa (M)

                                    q₂= θ à menentukan koordinat beban

 

Sistem 3

 

 

 

Pada sistem  3  

Koordinat umum         q₁= x                q₂= θ                q₃=l

 

b.        Nyatakan dalam T dan V dalam fungsi koordinat umum

v          ;

 

(V=0)

Sistem 1

 

 

 

 

 

 

 

 

 

        dimana

 

 

           dengan acuan Referensi T potensial V=0

 

Sistem 2

 

 

 

 

       dimana  maka

 

 

 

Sistem 3

 

 

Note :

 

 

c.    Tuliskan / Nyatakan dalam fungsi Lagrange

 

 

Ø  Sistem 1

 

Ø  Sistem 2

Ø  Sistem 3

 

 

d.    Berlakukan persamaan Lagrange (E-V)

 

Ø  Sistem 1

 

 

Ø  Sistem 2

                                                            -

 

Ø  Sistem 3